28届美国数学奥林匹克竞赛

第一部分（上午9：00-12：00）1999年4月271． nn的方格棋盘上放着一些棋子，满足如下两个条件：（a）　　　 放有棋子的方格和没有放棋子的方

第一部分（上午9：00-12：00）

1999年4月27

1． nn的方格棋盘上放着一些棋子，满足如下两个条件：

（a）　　　 放有棋子的方格和没有放棋子的方格有一条公共边。

（b）　　　 任意给定两个放有棋子的方格，可以标出一条路线，从其中一个给定的方格出发，经过所有放有棋子的方格，最后到达另一个给定的方格。如图：

求证：棋盘上至少有（n2-2）/3个棋子。

2． 求证：对于循环四边形ABCD有：|AB-CD| |AD-BC|2|AC-BD|。

3． 已知：p是大于2的质数，整数a、b、c、d不能被p整除，

且有{ra/p} {rb/p} {rc/p} {rd/p}=2 ，其中r是任一不能被p整除的整数。

求证：在（a b）、（a c）、（a d）、（b c）、（b d）、（c d）6个数中至少有两个能被p整除。

第二部分（下午1：00-4：00）

1999年4月27

4． 已知：实数a1a2 。。。an（n3）满足：a1 a2 。。。 ann，a12 a2 2 。。。 an2n2。

求证：max（a1a2 。。。an）2。

5． Y2K游戏：有2000千个方格排成一排,两个玩家轮流在方格里写S或O，谁先在连续的三个方格里写出SOS，谁就获胜；如果没有人写出算平局。

证明：后写的人有胜算。

6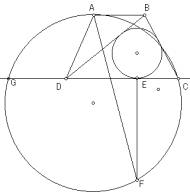． 已知：等腰梯形ABCD，AB//CD，△BCD的内切圆与CD交于E点；F是DAC的平分线上一点，且EFCD；△ACF的外接圆与CD交于C和G；

求证：△AFG是等腰三角形。

（

特别说明：由于各方面情况的不断调整与变化，360高考网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。如有出入，欢迎大家予以指正！

【挑错 】【推荐】【打印】