抽屉原则
大家知道，两个抽屉要放置三只苹果，那么一定有两只苹果放在同一个抽屉里，更一般地说，只要被放置的苹果数比抽屉数目大，就一定会有
大家知道，两个抽屉要放置三只苹果，那么一定有两只苹果放在同一个抽屉里，更一般地说，只要被放置的苹果数比抽屉数目大，就一定会有两只或更多只的苹果放进同一个抽屉，可不要小看这一简单事实，它包含着一个重要而又十分基本的原则抽屉原则.
1． 抽屉原则有几种最常见的形式
原则1 如果把n k(k1)个物体放进n只抽屉里，则至少有一只抽屉要放进两个或更多个物体：
原则本身十分浅显，为了加深对它的认识，我们还是运用反证法给予证明；如果每个抽屉至多只能放进一个物体，那么物体的总数至多是n，而不是题设的n k(k1)，这不可能.
原则虽简单.巧妙地运用原则却可十分便利地解决一些看上去相当复杂、甚至感到无从下手的总是，比如说，我们可以断言在我国至少有两个人出生的时间相差不超过4秒钟，这是个惊人的结论，该是经过很多人的艰苦劳动，统计所得的吧！不，只须我们稍动手算一下：
不妨假设人的寿命不超过4万天（约110岁，超过这个年龄数的人为数甚少），则
10亿人口安排在8亿6千4百万个抽屉里，根据原则1，即知结论成立.
下面我们再举一个例子：
例1 幼儿园买来了不少白兔、熊猫、长颈鹿塑料玩具，每个小朋友任意选择两件，那么不管怎样挑选，在任意七个小朋友中总有两个彼此选的玩具都相同，试说明道理.
解 从三种玩具中挑选两件，搭配方式只能是下面六种：
（兔、兔），（兔、熊猫），（兔、长颈鹿），（熊猫、熊猫），（熊猫、长颈鹿），（长颈鹿、长颈鹿）
把每种搭配方式看作一个抽屉，把7个小朋友看作物体，那么根据原则1，至少有两个物体要放进同一个抽屉里，也就是说，至少两人挑选玩具采用同一搭配方式，选的玩具相同.
原则2 如果把mn k(k1)个物体放进n个抽屉，则至少有一个抽屉至多放进m 1个物体.证明同原则相仿.若每个抽屉至多放进m个物体,那么n个抽屉至多放进mn个物体,与题设不符，故不可能.
原则1可看作原则2的物例（m=1）
例2正方体各面上涂上红色或蓝色的油漆（每面只涂一种色），证明正方体一定有三个面颜色相同.
证明把两种颜色当作两个抽屉，把正方体六个面当作物体，那么6=22 2，根据原则二，至少有三个面涂上相同的颜色.
例3 把1到10的自然数摆成一个圆圈，证明一定存在在个相邻的数，它们的和数大于17.
证明 如图12-1，设a1，a2，a3，，a9，a10分别代表不超过10的十个自然数，它们围成一个圈，三个相邻的数的组成是（a1，a2，a3），（a2，a3，a4），（a3，a4，a5），,（a9，a10，a1）,（a10，a1，a2）共十组.现把它们看作十个抽屉，每个抽屉的物体数是a1 a2 a3，a2 a3 a4，a3 a4 a5，a9 a10 a1，a10 a1 a2,由于
（a1 a2 a3） （a2 a3 a4） （a9 a10 a1） （a10 a1 a2）
=3(a1 a2 a9 a10)
=3(1 2 9 10)
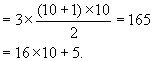
根据原则2,至少有一个括号内的三数和不少于17,即至少有三个相邻的数的和不小于17.
原则1、原则2可归结到期更一般形式：
原则3把m1 m2 mn k(k1)个物体放入n个抽屉里，那么或在第一个抽屉里至少放入m1 1个物体，或在第二个抽屉里至少放入m2 1个物体，，或在第n个抽屉里至少放入mn 1个物体.
证明假定第一个抽屉放入物体的数不超过m1个，第二个抽屉放入物体的数不超过m2个，，第n个抽屉放入物体的个数不超过mn，那么放入所有抽屉的物体总数不超过m1 m2 mn个，与题设矛盾.(责任编辑：www.360gaokao.com)
特别说明：由于各方面情况的不断调整与变化，360高考网所提供的所有考试信息仅供参考，敬请考生以权威部门公布的正式信息为准。如有出入，欢迎大家予以指正！
【挑错 】【推荐】【打印】
